[논문리뷰] SphereFace 설명 (Deep Hypershpere Embedding for Face Recognition)

[논문리뷰] SphereFace 설명 (Deep Hypershpere Embedding for Face Recognition)

개요

안녕하세요. 오늘은 얼굴 인식 관련 논문 중 2017년에 나온 SphereFace 논문에 대해 리뷰하겠습니다.

우선 얼굴인식 모델의 목표를 알아야 하는데요, 아래 그림과 같이 Closed-set과 Open-set에 대해 이해해야 합니다.

Closed-set은 Training Set과 Test Set의 분류해야 할 Class가 같은 것인데요, 예를 들어 강아지/고양이를 분류하는 Training set으로 학습했다면 Test set도 강아지/고양이로만 되어있습니다.

반면에, Open-set은 강아지/고양이로 학습했지만 Test는 호랑이/사자를 분류하게 되는 경우입니다. 즉, 특정 class의 feature를 학습한다기 보다는 서로 다른 class의 feature끼리는 유사도가 낮고, 같은 class의 feature는 유사도가 높도록 학습해야 합니다. 이런 학습을 Metric Learning 이라고 합니다.

얼굴인식에서는 학습할 수 있는 얼굴은 제한되어있지만 실제 응용하기 위해서는 학습에 사용되지 않은 새로운 얼굴도 구별할 수 있는 고유한 feature를 만들 수 있어야 하므로 Metric Learning에 적합하다고 볼 수 있습니다.

SphereFace는 이러한 학습을 위해 A-Softmax Loss라는 새로운 Loss를 제안합니다.

A-Softmax Loss

기존의 softmax 계산식은 아래와 같습니다.

$p_i = \dfrac{exp(\bold W_i^T\bold x+b_i)}{\sum_jexp(\bold W_j\bold x+b_j)}$

• $\bold x$는 모델의 학습된 출력 feature입니다.

• $\bold W_i, b_i$는 마지막 Fully Connected Layer의 Weight와 bias 입니다.

Binary Classification의 경우를 가정하여 $p_1, p_2$만 있다고 가정해보겠습니다. 그럼 $p_1>p_2$인 경우는 class1으로 예측 할 것이고, 반대인 경우에는 class2로 예측하게 됩니다.

이때, 두 개의 class를 결정하는 decision boundary는

$(\bold W_1-\bold W_2)\bold x+b_1-b_2=0$ 가 됩니다.

위의 식에서 $\|\bold W\|=1$이 되도록 normalize 해주고 $b_i=0$으로 두면 $\bold W_i^T\bold x=\|\bold W_i^T\| \|\bold x\|cos(\theta_i)$이므로 decision boundary를 아래 식으로 다시 표현할 수 있습니다.

$cos(\theta_1)\|\bold x\|-cos(\theta_2)\|\bold x\|=0$

($\theta_i$는 $\bold x$와 $\bold W_i$ 사이의 각도입니다.)

feature $\bold x$는 같으므로 실제로 두 개의 class를 구분하는 것은 $\theta_1$과 $\theta_2$라고 할 수 있습니다.

즉, 다시 말해 feature $\bold x_i$와 $\bold W_j$사이의 각도 $\theta_{j,i}$에 따라 class를 분류하게 됩니다.

이에 따라 softmax loss 식을 아래와 같이 다시 표현한 것을 Modified Softmax라고 합니다.

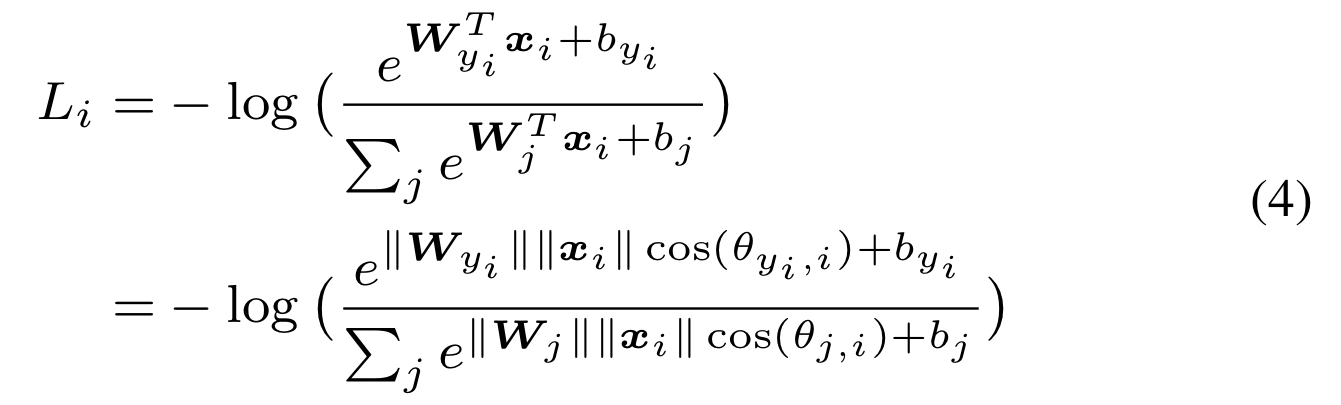
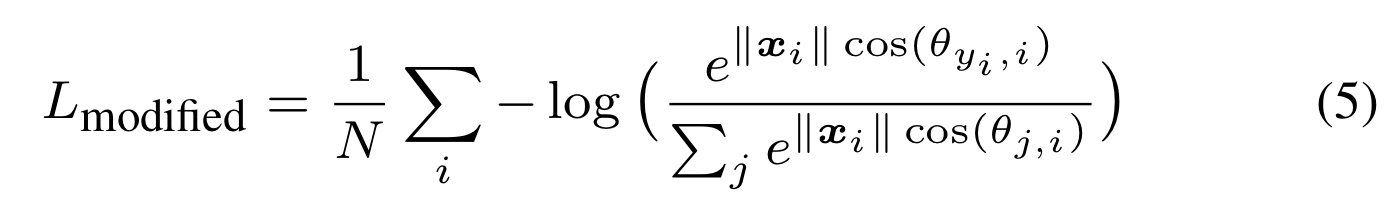
여기서 A-Softmax는 두 개의 $\theta_1$과 $\theta_2$가 더 잘 구분 될 수 있도록 angle 관점에서 margin을 주는 것입니다.

즉, 기존$cos(\theta_1)>cos(\theta_2)$에서 $cos(m\theta_1)>cos(\theta_2)$ 또는 $cos(\theta_1)>cos(m\theta_2)$과 같은식으로 margin값 m을 줍니다.

그럼 위의 softmax 식은 아래와 같이 다시 표현하게 됩니다.

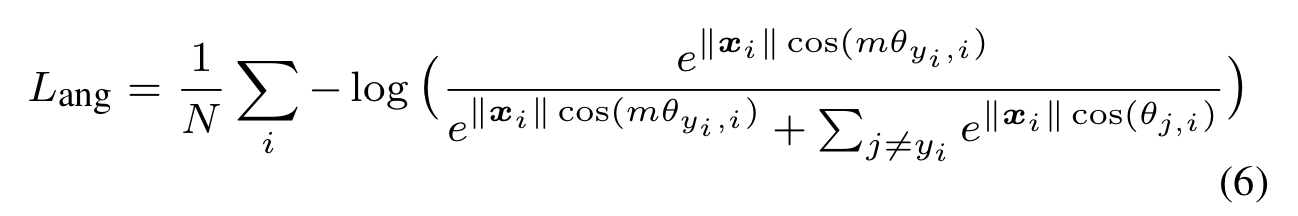
지금까지 나온 Loss에 대해 다시 살펴보면 아래와 같은 Decision Boundary를 갖게 됩니다.

이에 따른 feature들의 분포를 보면 아래 그림처럼 됩니다. original softmax를 쓰게 되면 margin이 없기 때문에 decision boundary(angular bisector)가 정확하게 두 개의 클래스를 분류하지 못합니다.(a)(b) 두번째로 margin이 없는 Modified Softmax loss를 보면 각도를 기준으로 분류하기 때문에 나름 잘 분류가 됩니다.(c)(d) 여기서 margin을 준 A-softmax Loss를 보면 두 개의 W1, W2가 각도를 기준으로 서로 멀리 떨어져 있기 때문에 가장 discriminative한 것을 확인할 수 있습니다.(d)(e)

아래는 다시 Loss에 따라 feature들이 어떻게 분포되는지 보여줍니다. A-Softmax Loss일 때 가장 명확한 분류가 되는것을 다시 한 번 확인할 수 있습니다.

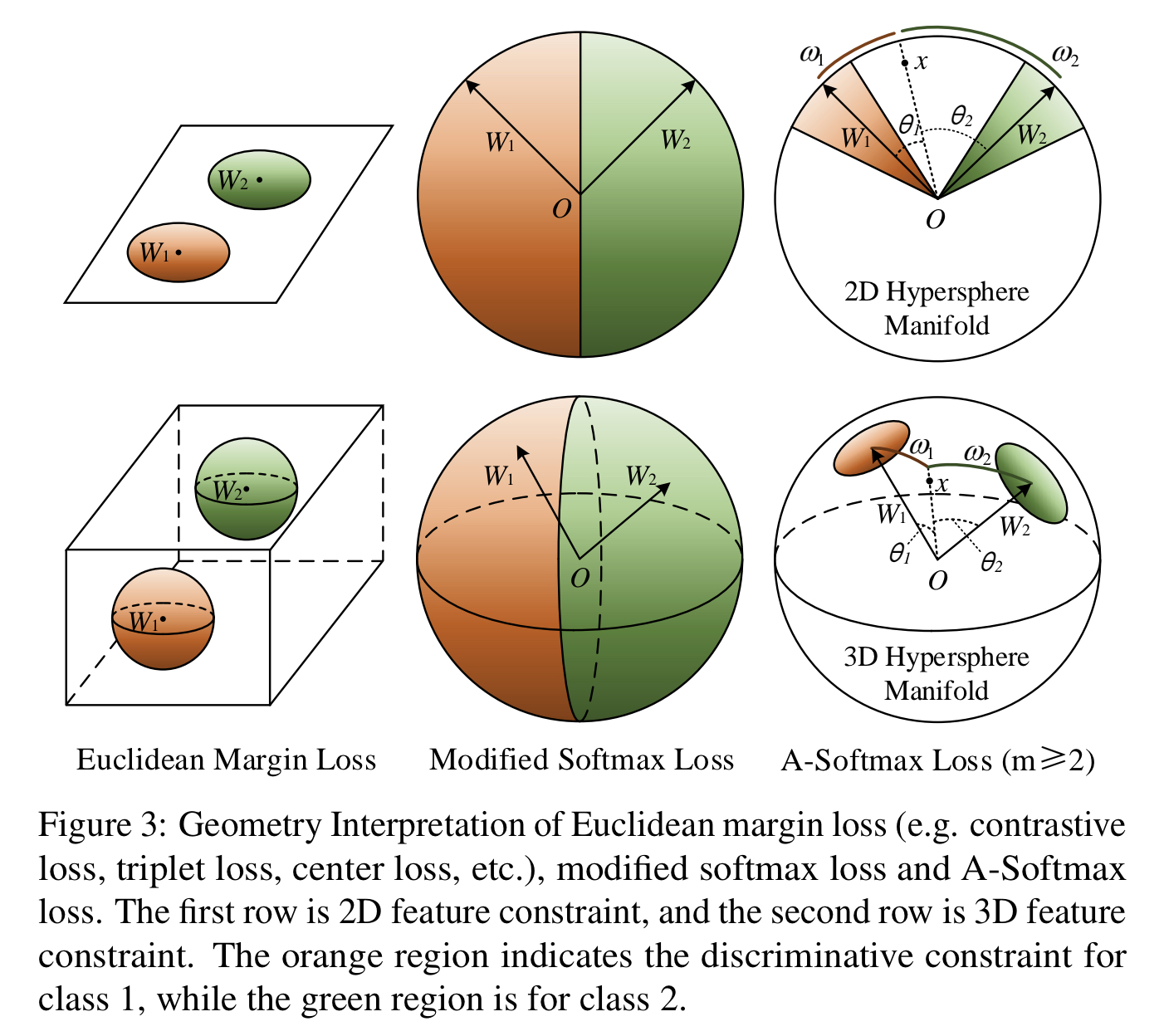
결론

처음에 얼굴 인식을 하기 위해선 같은 사람의 얼굴(inter-class variance)은 같이 분포해야 하고, 다른 사람의 얼굴끼리는(intra-class variance) 멀리 분포해야 한다는 목표가 있었습니다.

SphereFace에서 제안하는 A-Softmax Loss는 이에 적합한 방법론으로 angle 관점에서 어떻게 discriminative한 feature를 뽑을 수 있는지를 보여준 것 같습니다.

하지만 이후에 margin을 줄 수 있는 더 좋은 방법론들이 제시 되면서 A-Softmax Loss의 한계가 있음을 지적합니다. 추후에 이와 관련된 논문들을 리뷰해보겠습니다.